出版物
地震動シミュレーションのための数値解析手法の開発
情報環境学専攻(教授) 廣瀬 壮一
1. 境界要素法を用いた異方性飽和多孔質弾性体に対する波動伝播・散乱シミュレーション
水で飽和した地盤・岩盤中を伝播する地震動の伝播・散乱を想定し,異方性飽和多孔質弾性体の2次元面内波動問題に対する数値解析手法の開発を行った.地盤・岩盤はBiotによって提案された異方性飽和多孔質弾性体モデルを用い,解析手法は演算子積分時間領域境界要素法を用いた.
地盤・岩盤を伝播する地震動は材料異方性,多孔質構造および間隙流体の影響を受ける.そのため,地盤・岩盤は固体と液体で構成される二相体と考えることができる.一般に,この様な媒質は,異方性飽和多孔質弾性体と呼ばれ,その力学モデルはBiotによって提案されている.Biotによる異方性飽和多孔質弾性体中では,偏向した2種類の縦波(qP1,qP2波)と2種類の横波(qS1,qS2波)の合計4種類の位相速度の異なる波動が存在し,これらの波動は流体の粘性によるエネルギー散逸を生じることが知られている.
境界要素法は,波動解析に有効な数値解析手法として知られる.飽和多孔質弾性体に対する境界要素法は,これまでいくつかの適用例が報告されており,その多くは,Biotの飽和多孔質弾性体モデルを用いている.しかし,Biotの飽和多孔質弾性体モデルでは,周波数に依存した分散・散逸性を有する波動を取り扱うため,時間領域での基本解の表現が困難となる.そのため,境界要素法の適用例の多くは周波数領域の解析であり,時間領域の解析例はほとんど報告されていない.演算子積分時間領域境界要素法は,時間領域境界積分方程式に含まれる畳み込み積分の計算に,演算子積分法を用いた新しい時間領域境界要素法である.この解析手法の最大の特徴に,時間領域解法でありながら,ラプラス像空間における基本解を用いる点がある.そのため,この解析手法を用いれば,時間領域基本解が求まらない問題に対しても,時間領域の解析が可能となる.なお,境界要素法では対象とする媒質および物理現象に対応する基本解が必要となる.異方性飽和多孔質弾性体の波動問題では,これに対応する基本解に関する報告例がほとんど存在しないため,本研究ではこれを独自に導出し,解析に用いた.
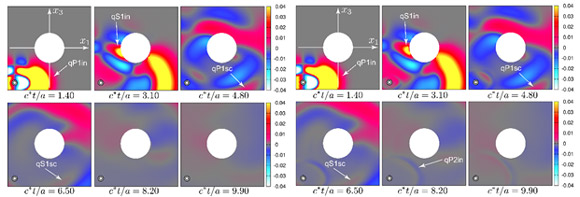
図1に異方性飽和多孔質弾性体中の空洞による入射波の散乱問題の解析結果を示す.本研究では間隙流体の粘性を考慮した場合とゼロと仮定した場合の解析結果の比較を行った.これらの結果から,間隙流体の粘性は,媒質中を伝播する4種類の波動のうち,特に遅い縦波(qP2波)の伝播・散乱に強い影響を与えることが確認された.これは,qP2波が他の3種類の波動と異なり,間隙流体の移動を伴う波動であることが原因であると考えられる.
Furukawa, A., Chikazawa, F., Saitoh, T. and Hirose, S.: 2-D wave analyses for fluid-saturated porous solids using convolution quadrature boundary element method, 10CUEE, CD-ROM収録, 2013.
 |
|
| (a) 間隙流体の粘性を考慮した場合 | (b) 間隙流体の粘性をゼロと仮定した場合 |
図1 空洞周辺の変位場の時間変化(砂岩) |
|
2. 高速多重極法を用いた演算子積分時間領域境界要素法の高速化
地震動シミュレーションでは大規模波動問題を取り扱うことも多いため,高速多重極法を演算子積分時間領域境界要素法に適用し,計算時間の短縮および記憶容量の軽減に関する検討を行った.この結果から,高速多重極法を適用することで,演算子積分時間領域境界要素法による大規模波動解析が可能となることが確認された.
例えば,Hirose, S. and Saitoh, T.: Parallelized fast multipole BEM for seismic analysis in time-domain, 7CUEE & 5ICEE, pp.1537-1542, 2010
